Description

\( \newcommand{\R}{\mathbb{R}} \newcommand{\dx}{\mathrm{d}} \)
The Fokker Planck equation has the form
\[
\partial_t \varrho(x,t) = \nabla \cdot \bigl(\beta^{-1} \nabla \varrho(x,t) + \varrho(x,t) \nabla H(x)\bigr) ,\qquad \varrho(x,0)=\varrho_0(x) ,
\] where \(H:\R^n\to \R\) is a smooth function, \(\beta>0\) some parameter and \(\varrho_0\) a probability density on \(\R^n\). The partial differential equation is in divergence form and conserves mass. Hence, also \(\varrho(\cdot,t)\) is a probability density on \(\R^n\). In the case, where \(H\) has some growth at \(\infty\), the equilibrium solutions \(\varrho_\infty:\R^n \to \R\) are characterized by
\[ \beta \nabla \varrho_\infty + \varrho_\infty \nabla H =0 \] leading to the solution
\[ \varrho_\infty(x) = Z^{-1} e^{-\beta H(x)} \quad \text{with} \quad Z = \int e^{-\beta H(x)} \; \dx x \]
The density \(\varrho_\infty\) is called Gibbs distribution, which accounts to the fact, that it minimizes the (Gibbs) free energy
\[ F(\varrho) = E(\varrho) + \beta^{-1} S(\varrho) \] where \(E\) is the energy and \(S\) the (Gibbs-Boltzmann) entropy
\[ E(\varrho) := \int H \varrho\;\dx x \quad\text{and}\quad S(\varrho) := \int \varrho \log \varrho \; \dx{x} . \] By this formulation  \(\beta\) plays the role of the inverse temperature. Note, that the Euler-Lagrange equation is given by
\[ H(x) + \beta^{-1} \bigl(\varrho(x) + 1\bigr) = 0 , \] which is solved by \(\varrho_\infty\).

Pathwise formulation via stochastic differential equations

The stochastic process \(X(t)\) defined by
\[ \dx X(t) = – \nabla H(X(t))\;\dx t + \sqrt{2\beta^{-1}} \;\dx W(t) , \quad X(t) = X_0 , \] where \(W(t)\) is an \(n\)-dimensional Brownian motion, is the pathwise formulation of the Fokker Planck equation. If distribution of the initial random vector \(X_0\) is given by \(\mathrm{law}\; X_0 = \varrho_0\), then at later times the solution \(X(t)\) has distribution \(\mathrm{law}\; X(t) = \varrho(\cdot,t)\), where \(\varrho\) is solution of the Fokker Planck equation.

The dynamic of the pathwise formulation undergoing diffusion in the potential \(H\). The particle is solely described by its position \(X(t)\in \R^n\), i.e. inertia is neglected. Then, the particle chooses the steepest descent with respect ot \(H\), which is perturbed by random fluctuation, which are assumed to be normal distributed. The coupling parameter \(\beta\) describing the strength of the fluctuations plays again the role of inverse temperature. In particular, the limit \(\beta\to \infty\) describes the behaviour of the system without fluctuations.

Ornstein-Uhlenbeck process

A prominent example, which can be explicitly solved, is the Ornstein-Uhlenbeck process, corresponding to the choice
\[ H(x) = \frac{\gamma}{2} | x |^2 . \] The stationary distribution is given by the Gaussian
\[ \varrho_\infty(x) = \left( \frac{2\pi}{\gamma\beta} \right)^{-\frac{n}{2}} \exp\left(-\frac{\gamma \beta |x|^2}{2}\right) . \] The underlying picture becomes particular simple in one dimension. There, the leading order behaviour of the process can be characterized by its mean \(m(t)\) and variance \(\sigma(t)\), which are given by
\[ m(t) := \int x \varrho(x,t) \;\dx x \qquad\text{and}\qquad \sigma(t) := \int (x-m(t))^2 \varrho(x,t) \;\dx{x} = \int x^2 \varrho(x,t)\; \dx{x} – m(t)^2 . \] Both, \(m(t)\) and \(\sigma(t)\), satisfy an ordinary differential equation not depending on \(\varrho\)
\[ \dot m(t) = -\gamma m(t) \qquad \text{and}\qquad \dot sigma(t) = 2\beta^{-1} – 2\gamma \sigma(t) .\] Hence, the mean converges exponentially fast to \(0\) with rate \(\gamma\) and the variance converges exponentially fast from the initial variance \(\sigma(0)\) to \((\beta \gamma)^{-1}\) with rate \(2 \gamma\)
\[ m(t) = m(0) \; e^{-2\gamma t} \qquad\text{and}\qquad \sigma(t) = \sigma(0) e^{-2\gamma t} + \frac{1}{\beta \gamma} \bigl(1-e^{-2\gamma t}\bigr) . \]

Numerical example

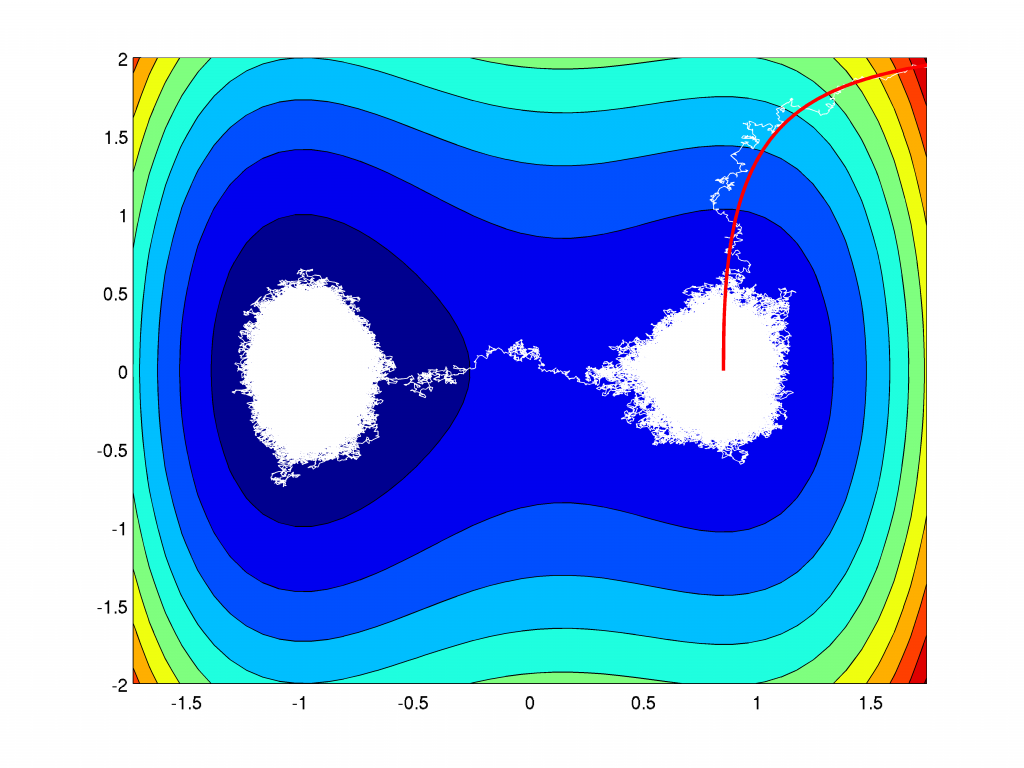
For general potentials \(H\) explicit solutions of the Fokker Planck equation are not available. However, the pathwise formulation allows to do Monte-Carlo simulation of single realisations of the process \(X(t)\). The case, where \(H\) is not convex is especially interessting, because at low temperature, i.e. \(\beta \gg 1\), the process shows metastable behaviour.

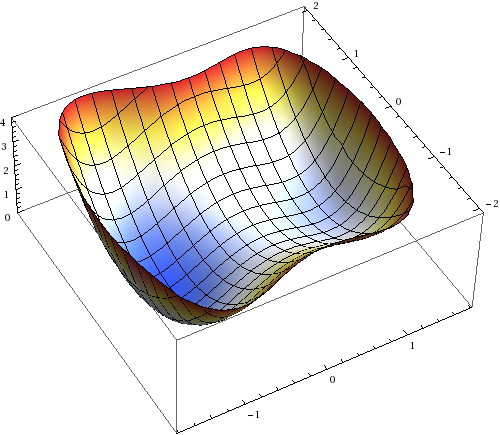
Therefore, we consider the potential function \(H:\R^2 \to \R\) looking like

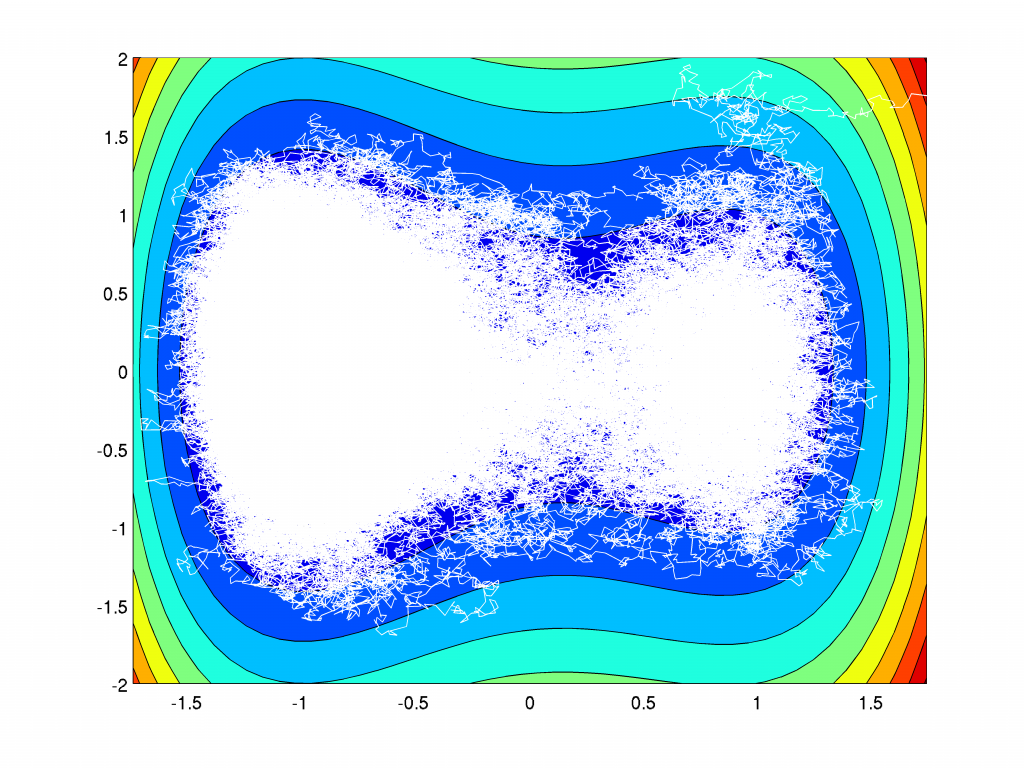
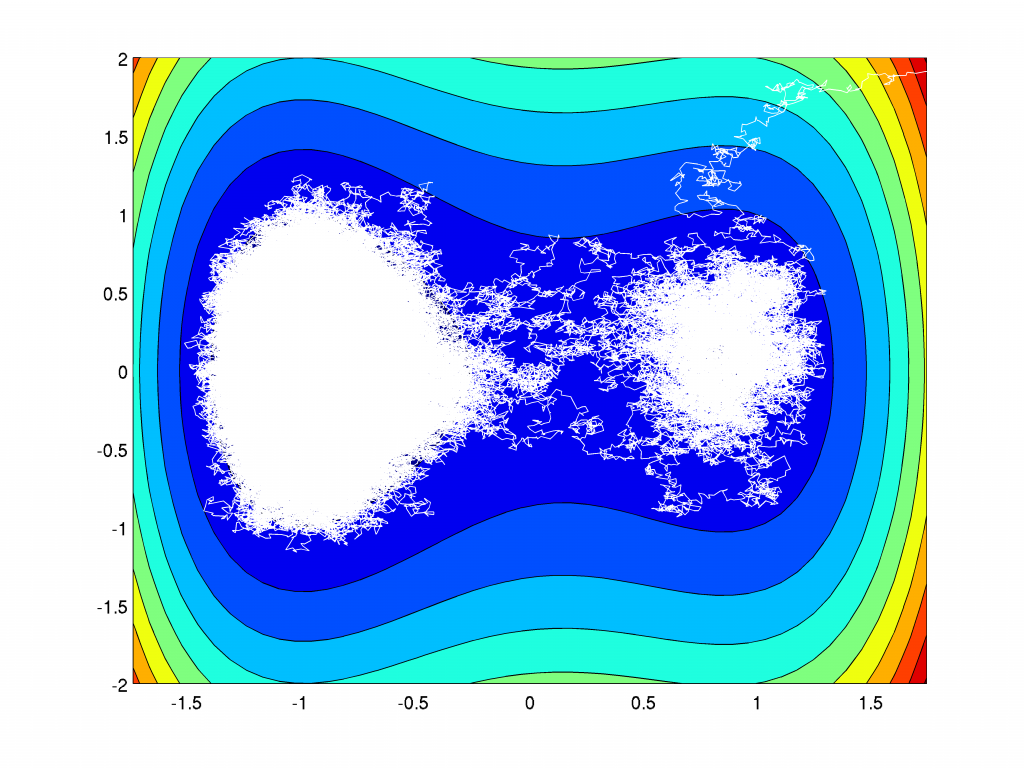
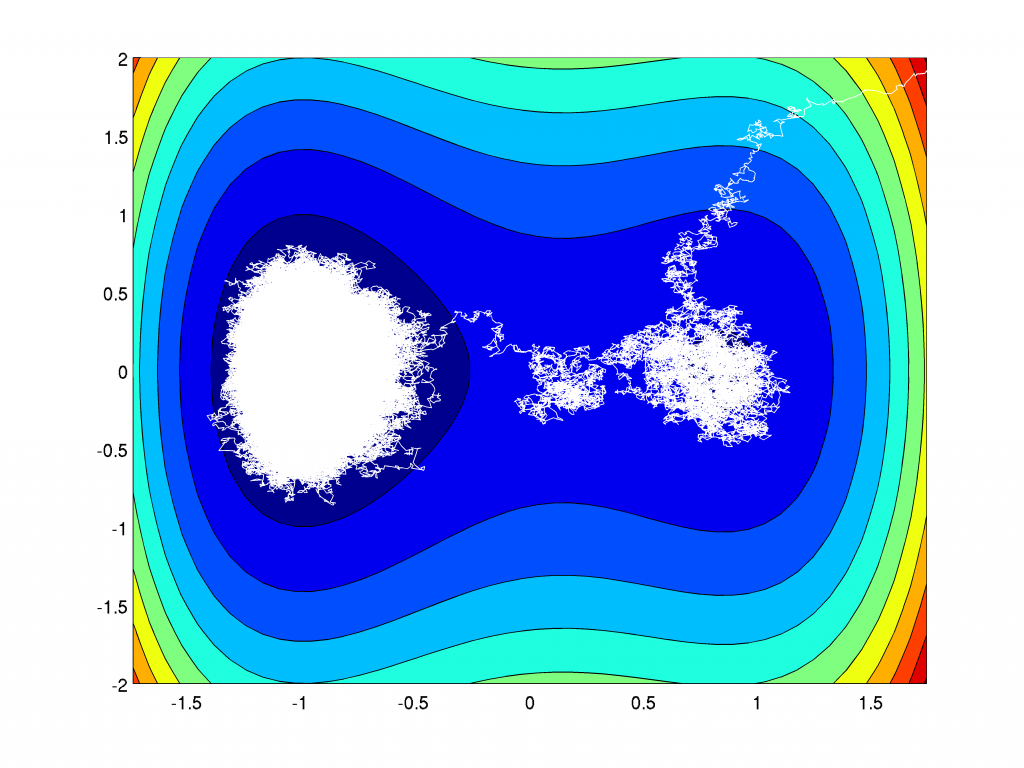
The realization of the process \(X(t)\) for increasing values of \(\beta\):

Monte Carlo simulation for Fokker Planck equation \(\beta=2.5\)

Monte Carlo simulation for Fokker Planck equation \(\beta=5\)

Monte Carlo simulation for Fokker Planck equation \(\beta=10\)

Monte Carlo simulation for Fokker Planck equation \(\beta=20\) (red \(\beta=\infty\))

For increasing values of \(\beta\) the particle goes quickly to the local minima and is trapped there longer and longer times. The transition to the global energy minimizing state happens along a path crossing the saddle. This behaviour is called metastable. For the limiting dynamic \(\beta=\infty\) without any fluctuation a transition is not possible and the particle is stuck in the local minima.

References

1. R. Jordan, D. Kinderlehrer, and F. Otto, “The Variational Formulation of the Fokker-Planck Equation,” SIAM Journal on Mathematical Analysis, vol. 29, no. 1, 1998.